Exhaustive Search
완전탐색은 무식하게 문제를 풀어나가는 방식이라고 하는데, 필자 생각에는 무식하다는 표현은 어울리지 않는 것 같다. 대부분의 알고리즘 문제는 완전탐색으로 다 풀수 있을 정도로 강력한 방식이다. 물론 그래서 무식하다고 부를 수 있지만 사실 컴퓨팅 성능이 미친듯이 좋으면 어떤알고리즘을 쓰더라도 빠르게 결과를 볼 수 있다. 그래서 무식한 방법이라고 절대 무시하면 안된다.
완전탐색을 문제를 해결하기 위한 모든 경우의 수를 나열하고, 정답을 찾아가는 방법을 의미한다. 완전탐색에는 Brute-Force, Bitmask, Recursive Fuction, Permutation, BFS, DFS 알고리즘이 있다. 완전탐색은 탐색의 방법론을 의미하고 그 안에 다양한 알고리즘들이 있다.
Brute-force
그냥 정말 단순하게 반복문(for, while)과 조건문(if, switch)을 사용하여 모든 경우의 수를 구현하는 방법이다. 단순한 방법론이기 때문에 단독으로 사용되는 경우는 없다라고 할 수 있다. 그냥 코드 곳곳에 낑겨 들어가있다.
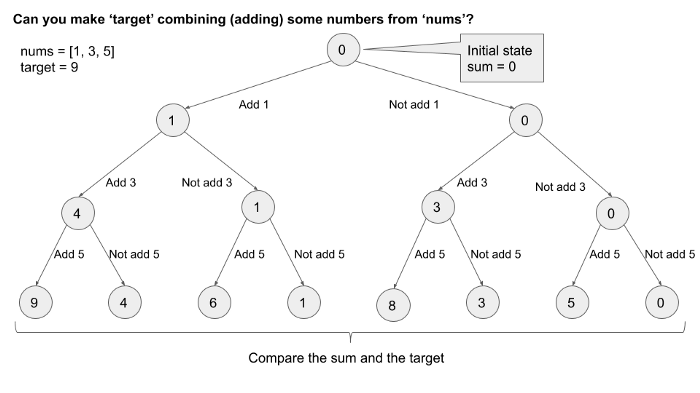
위 그림처럼 nums를 조합해서 9를 만들 수 있는지 없는지 알아보기 위해 위와 같은 알고리즘을 구상할 수 있다. 존재할 수 있는 모든 경우의 수를 다 따져본다음에 확인해보는 방식을 의미한다.
Bitmask
bit라는 단어를 보면 바로 떠오르는 것이 있을 것이다. 바로 2진수. bitmask는 2진수를 이용하여 연산하는 방식이다. 2진수를 어떻게 활용하는지 확인해보도록 하겠다.
길이가 4인 [1, 2, 3, 4] 리스트가 존재한다고 가정한다. 여기서 몇가지 값을 뽑아 부분집합을 만들어보려고 한다.
(1), (2), (3), (4), (1, 2), (1, 3) ...대충 이렇게 많은 경우의수가 존재할 수 있다. 지금은 리스트의 길이가 4여서 크게 무리는 없지만 만약에 200이라면? 말이 달라진다. 엄청난 메모리가 소모될 것이고 오버헤드가 발생할 확률이 높다.
이때 바로 bitmask를 사용하여 좀더 효율적으로 표현할 수 있다.
[ 1, 2, 3, 4 ]
--------------
1 1 1 1
1 1 1 0
1 1 0 1
1 1 0 0
....리스트의 길이만큼에 해당하는 bit list 를 생성하고, 존재(1) 아니면 (0)으로 표기한다. 이것을 다시 10진수로 바꿔서 표현할 수도 있다.
그렇다면 부분집합을 배열이 아니라 정수로도 관리할 수 있다. 그리고 이때 바로 비트연산자를 통해서 삽입, 삭제, 조회 등을 효율적으로 진행할 수 있다.
Recursive Funtion
재귀함수를 사용해서 문제를 푸는 방법이다. 대체적으로 '중복이 없이 n개중 m개를 선택하는 방법'엘 대해서 재귀함수를 사용할 수 있다.
예를들어 3장의 카드 중에서 3장을 뽑는 경우의수가 있다라고 한다. 그렇다면 3중첩의 반복문을 사용해서 경우의 수를 구해야 한다. 바로 이때 재귀 호출을 통해서 코드를 간략하게 짤 수 있다.
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int k = j + 1; k < n; ++k) {
for (int l = k + 1; l < n; ++l) {
cout << i << " " << j << " " << k << " " << l << "\n";
}
}
}
}// picked: 지금까지 고른 원소들의 번호
// toPick: 더 고를 원소의 수
// 앞으로 toPick개의 원소를 고르는 모든 방법을 출력
void pick(int n, vector<int>& picked, int toPick) {
// 기저사례: 더 고를 원소가 없을 때 고른 원소들을 출력
if (toPick == 0) {
printPicked(picked);
return;
}
// 고를 수 있는 가장 작은 번호를 계산
int smallest = picked.empty() ? 0 : picked.back() + 1;
// 이 단계에서 원소 하나를 고른다
for (int next = smallest; next < n; ++next) {
picked.push_back(next);
pick(n, picked, toPick - 1);
picked.pop_back();
}
}
Permutation
완전탐색기법의 가장 대표적인 유형으로 그냥 뭐 모든 경우의 수 다 구하는 것이다. 딱히 특별한 내용은 없다...?
Reference
https://medium.com/@shoyataguchi/improve-brute-force-9e14b5105c0d
Improve Brute Force
Naive brute-force algorithms and their improvements will be explained.
medium.com
https://inyongs.tistory.com/93
무식하게 풀기 (완전 탐색)
무식하게 풀기 (완전 탐색) 완전 탐색? 가능한 방법을 전부 만들어 보는 알고리즘 재귀 호출과 완전 탐색 문제를 들여다볼수록 각 조각들의 형태가 유사해지는 작업. 이런 작업을 구현할 때
inyongs.tistory.com
'ALGORITHM > Algorithm 설명' 카테고리의 다른 글
| [알고리즘] BFS (Breadth First Search) (0) | 2022.02.04 |
|---|---|
| [알고리즘] DFS (Depth First Search) (0) | 2022.02.03 |
| [알고리즘] Queue (0) | 2022.01.19 |
| [알고리즘] Stack (0) | 2022.01.18 |
| [알고리즘] 해시 테이블 (Hash Table) (0) | 2022.01.12 |



