너비우선탐색
그래프를 전체 탐색하는 방법 중 너비우선탐색은 DFS와 다르게 루트노드에 인접한 노드들 부터 먼저 탐색하고 그 다음으로 가까운 노드를 탐색하는 구조이다. 즉 정점에 가까운 노드들을 먼저 순회하고, 먼 노드는 나중에 순회하게 된다. 이러한 특징으로 인해서 일반적으로 두 노드 사이의 최단 경로를 찾고 싶을때 사용한다. 구현으로써는 큐를 이용한다.
 |
장점
트리의 깊이가 얕은 경우에 매우 빠르게 동작할 수 있는 알고리즘이다. 더불어 단순하게 생각하면 깊이우선탐색보다 너비우선탐색이 더 빠르다. 또한 루트노드와 가까운 노드부터 탐색하기 때문에 최단경로를 보장할 수 있다.
단점
너비우선탐색은 깊이우선탐색보다 많은 메모리를 필요로 한다. 왜냐하면 다음에 탐색할 정점들을 알고있어야 하기 때문이다. 또한 노드의 개수가 증가하면 그만큼 탐색해야 하는 노드도 많아진다.
구현방법
BFS는 리스트를 사용해서 구현할 수 있다. 구현에 대한 예제소스는 하단 레퍼런스엥 걸려있는 블로그를 참고하였다 (감사합니다).

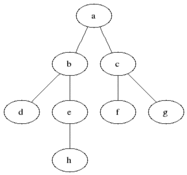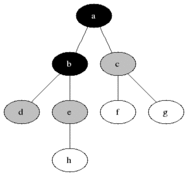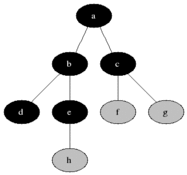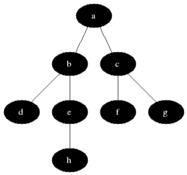
위와 같은 그래프가 존재한다고 가정해보도록 하겠다. A부터 K까지의 노드로 연결되어있고 방향성은 존재하지 않는다. BFS는 시작노드와 인접한 노드들부터 탐색을 진행한다.
# 파라미터
# graph: 그래프를 표현하고 있는 딕셔너리(혹은 리스트도 가능)
# start_node: 시작 노드 정보
def bfs(graph, start_node):
# 방문이 필요한 노드를 관리하기 위한 리스트 생성
need_visited = []
# 방문을 완료한 노드들을 관리하기 위한 리스트 생성
visited = []
# 방문이 필요한 노드를 관리하는 리스트에 시작노드 삽입
need_visited.append(start_node)
# 반복문을 통해서 방문이 필요한 노드를 방문
while need_visited:
# 방문이 필요한 노드들을 관리하는 리스트의 0번째 요소 추출
node = need_visited[0]
del need_visited[0]
# 추출된 노드가 한번도 방문된 적이 없다면
if node not in visited:
# 노드를 방문하고
visited.append(node)
# 이 노드와 연결되어있는 다른 노드들을 방문이 필요한 노드를 관리하는 리스트에 추가한다.
need_visited.extend(graph[node])
return visited리스트를 사용해서 방문을 진행하였지만 사실 큐의 방식을 이용한거나 마찬가지이다.
예제
BFS 문제를 많이 풀어본건 아니지만 그래프가 다음과 같이 주어지는 상황이 있기도 하다. DFS로 풀수 있는 문제는 BFS로도 풀 수 있다고 하는데, 모든 문제가 다 그런지는 모르겠다.

참고로 이 문제는 백준의 2606 바이러스 문제이다. 위와 같이 문제가 주어지고 예제 입력으로는 다음과 같이 주어진다.

이때 세번째줄부터 마지막줄까지 노드들의 연결성을 나타내고 있다. 위를 통해서 그래프를 만들어주면 된다. 이번 문제의 경우는 방향성이 존재하지 않기 때문에 1번에서 연결되어있는 애들 모두, 2번에서 연결되어있는 모든 노드를 리스트로 표현해줄 것이다.
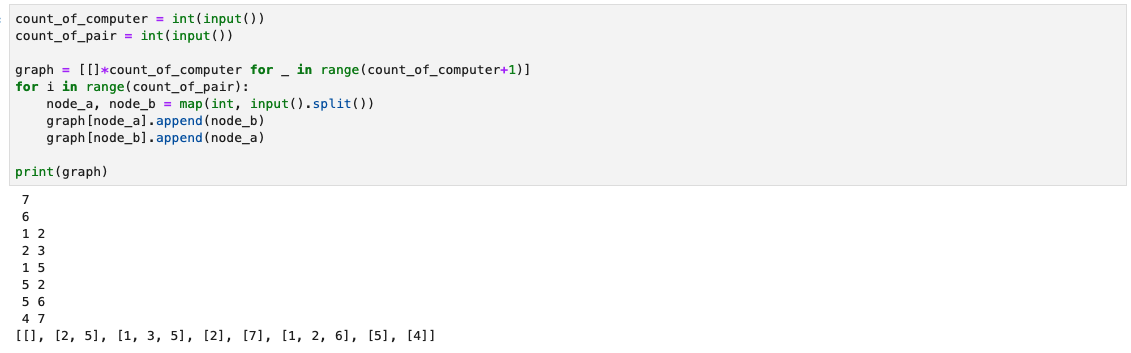
위사진과 같이 graph리스트를 만들고 이걸로 그래프를 표현하였다. 리스트의 인덱스번호를 컴퓨터 번호로 생각하면 되고, 요소 안의 리스트는 연결되어있는 노드들을 나타낸다고 생각하면 된다. 반복문을 통해 graph 리스트를 채운다. 여기서 컴퓨터는 1번부터 시작하기 때문에 이해를 쉽게 하기 위해서 0번인덱스는 사용하지 않고 1번 인덱스부터 사용하였다.
count = 0
def bfs(graph, start, count_of_computer):
global count
need_visited = []
visited = []
need_visited.append(start)
while need_visited:
node = need_visited.pop(0)
if node not in visited:
visited.append(node)
need_visited.extend(graph[node])
count += 1
return visited
count_of_computer = int(input())
count_of_pair = int(input())
graph = [[]*count_of_computer for _ in range(count_of_computer+1)]
for i in range(count_of_pair):
node_a, node_b = map(int, input().split())
graph[node_a].append(node_b)
graph[node_b].append(node_a)
bfs(graph, 1, count_of_computer)
print(count-1)BFS 방식으로 구현하였기 때문에 리스트를 Queue와 같은 방식으로써 need_visited를 생성하여 사용하였다. 작동방식은 이전의 DFS에서 설명한것과 유사하하고 BFS이기 때문에 가까운 노드부터 탐색한다는 개념을 그대로 가져간다.
Reference
https://ko.wikipedia.org/wiki/%EB%84%88%EB%B9%84_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89
너비 우선 탐색 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
https://data-marketing-bk.tistory.com/45?category=901221
BFS 완벽 구현하기 - 파이썬
1. BFS 기본 개념 2. BFS 구현 원리 3. BFS 구현 코드 1. BFS 기본 개념 BFS란 그래프 자료 구조에서 원하는 자료를 찾는 탐색 알고리즘 중에 하나입니다. 자료를 찾을 때 "수직" 방향으로 자료를 검색할
data-marketing-bk.tistory.com
https://www.acmicpc.net/problem/2606
2606번: 바이러스
첫째 줄에는 컴퓨터의 수가 주어진다. 컴퓨터의 수는 100 이하이고 각 컴퓨터에는 1번 부터 차례대로 번호가 매겨진다. 둘째 줄에는 네트워크 상에서 직접 연결되어 있는 컴퓨터 쌍의 수가 주어
www.acmicpc.net
'ALGORITHM > Algorithm 설명' 카테고리의 다른 글
| [알고리즘] Binary Search (0) | 2022.02.28 |
|---|---|
| [알고리즘] Dynamic Programming (0) | 2022.02.15 |
| [알고리즘] DFS (Depth First Search) (0) | 2022.02.03 |
| [알고리즘] 완전탐색 (Exhaustive Search) (0) | 2022.01.25 |
| [알고리즘] Queue (0) | 2022.01.19 |



