Spanning Tree
그래프 내의 모든 정점을 포함하는 트리를 의미한다. 즉 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다. 신장트리는 코딩테스트에서 그리디 알고리즘 문제로 자주 출제되는 유형 중 하나라고 한다.

위 그림은 신장트리의 예시이며 모든 정점을 포함하면서 사이클이 존재하지 않는 구조를 띄고 있다. DFS, BFS를 이용하여 그래프에서 신장 트리를 찾을 수 있으며 여러모양의 신장트리가 존재할 수 있다. 따라서 신장 트리는 그래프에 있는 n개의 정점을 n-1개의 간전으로 연결하여야 한다. 신장트리는 일반적으로 통신 네트워크를 구축할때 사용되기도 한다.
Kruskal 알고리즘
신장트리에서 간선들의 가중치 합이 최소인 트리를 말한다. Minimum Spanning Tree (MST)라고 부른다. 각 간선의 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말한다. 즉 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것이다.
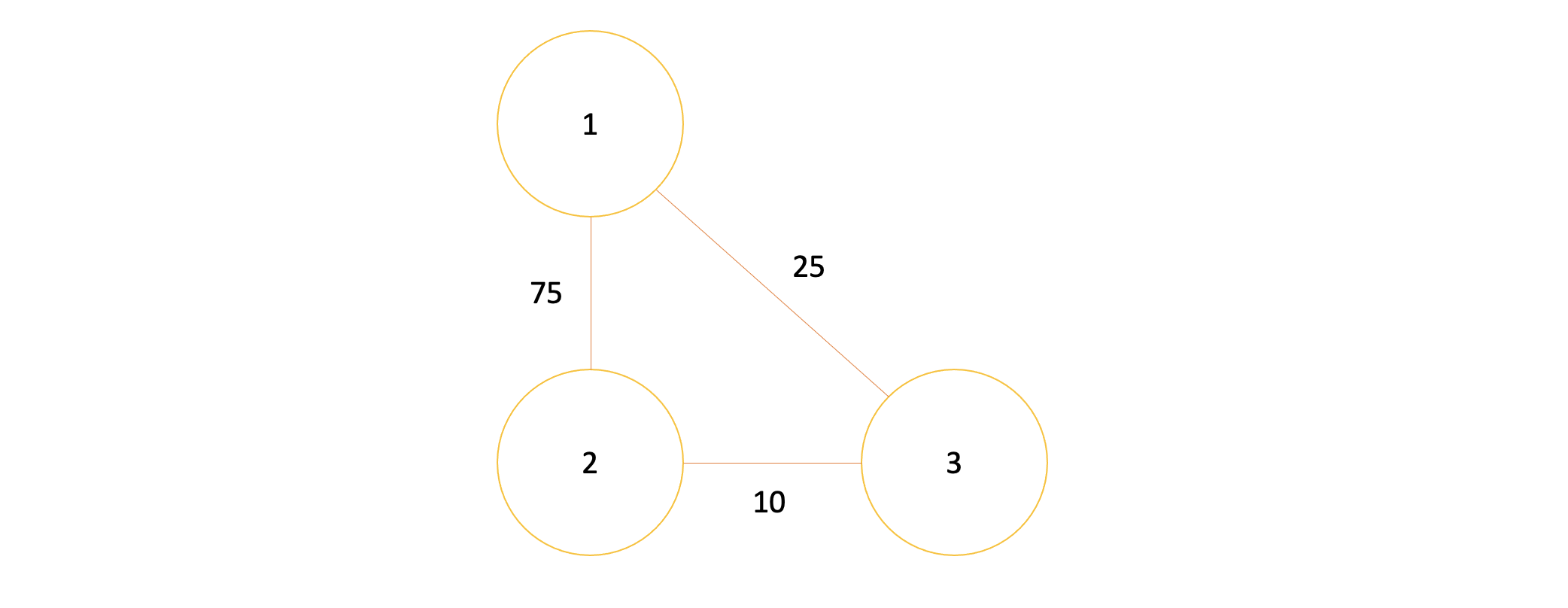
만약 위와 같은 그래프가 있을때 최소 비용으로 각 노드들을 연결해보도록 한다.
현재 그래프는 노드가 몇개 없어서 간단하다. 여기서 가능한 경우의 수는 3가지이다. 75 + 25, 10 + 25, 75 + 10 이다. 이때 10 + 25인 부분을 연결하게 되면 최소한의 비용으로 노드들을 연결할 수 있다. 여기서 2개의 간선만 이용한 이유는 신장트리에서 간선의 개수는 N-1, 즉 정점의 개수 - 1 개 이기 때문이다.
Kruskal Algorithm 구현
알고리즘의 작업 흐름은 다음과 같다.
- 비용에 따라 간선을 오름차순으로 정렬
- 간선을 하나씩 확인하면서 간선이 추가되었을때 사이클이 발생하는지 확인
- 사이클이 발생하지 않는 경우, 최소 신장 트리에 간선 추가
- 사이클이 발생하는 경우, 최소 신장 트리에 간선을 추가시키지 않음

v, e = map(int, input().split())
# 부모 테이블 초기화
parent = [0] * (v+1)
for i in range(1, v+1):
parent[i] = i
# find 연산
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# union 연산
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 간선 정보 담을 리스트와 최소 신장 트리 계산 변수 정의
edges = []
total_cost = 0
# 간선 정보 주어지고 비용을 기준으로 정렬
for _ in range(e):
a, b, cost = map(int, input().split())
edges.append((cost, a, b))
# 간선 정보 비용 기준으로 오름차순 정렬
edges.sort()
# 간선 정보 하나씩 확인하면서 크루스칼 알고리즘 수행
for i in range(e):
cost, a, b = edges[i]
# find 연산 후, 부모노드 다르면 사이클 발생 X으므로 union 연산 수행 -> 최소 신장 트리에 포함!
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
total_cost += cost
print(total_cost)
Reference
https://techblog-history-younghunjo1.tistory.com/262
[Python] 최소 신장 트리를 찾는 크루스칼(Kruskal) 알고리즘
🔊 이번 포스팅에는 최근에 Python으로 알고리즘을 공부하기 시작하면서 알게 된 여러 알고리즘의 원리와 Python으로 구현하는 방법에 대해 소개해보려 한다. 필자는 최근 알고리즘 공부를 '나동
techblog-history-younghunjo1.tistory.com
https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
[알고리즘] 최소 신장 트리(MST, Minimum Spanning Tree)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
https://katfun.tistory.com/entry/%EA%B7%B8%EB%9E%98%ED%94%84-%EC%9D%B4%EB%A1%A0
그래프 이론
그래프 자료구조는 코딩 테스트에서 난이도가 제법 있으면서도 어려운 부분입니다. 앞서 살펴본 DFS/BFS, 최단 경로 모두 그래프 자료구조를 활용합니다. 이 외에도 다양한 그래프 자료구조를 이
katfun.tistory.com
https://coding-factory.tistory.com/610
[Algorithm] 자료구조 그래프(Graph)란 무엇인가?
그래프란? 그래프는 정점과 간선으로 이루어진 자료구조입니다. 정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼수도 있겠습니다. 그런면에서 트리는 그래프의 일종인 셈입니다. 다만
coding-factory.tistory.com
[그래프 이론 알고리즘] 다양한 그래프 알고리즘
그래프 이론 알고리즘 - DFS/BFS 알고리즘과 최단 경로 알고리즘에서 다룬 내용은 모두 그래프 알고리즘의 한 유형 - 크루스칼 알고리즘은 그리디 알고리즘, 위상 정렬 알고리즘은 큐 자료구조 혹
s0ng.tistory.com
'ALGORITHM > Algorithm 설명' 카테고리의 다른 글
| [알고리즘] - 위상정렬 (0) | 2022.03.19 |
|---|---|
| [알고리즘] 서로소 집합 - Disjoint Sets (5) | 2022.03.18 |
| [알고리즘] 그래프 이론 (0) | 2022.03.18 |
| [알고리즘] 최단경로 알고리즘 (0) | 2022.03.12 |
| [알고리즘] Binary Search (0) | 2022.02.28 |



